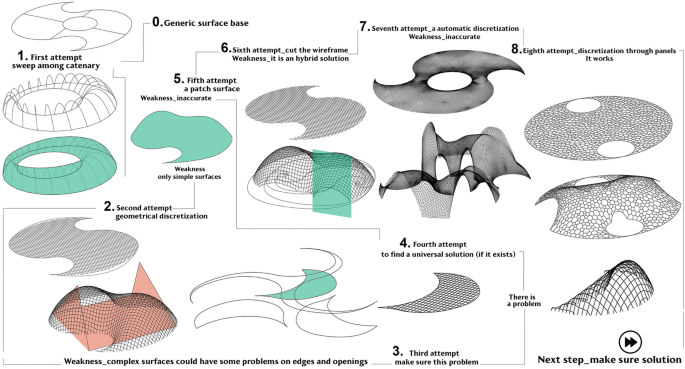
Degital Design Tool Voronoi Diagram
The role of the 3D physical model in optimized shape research is the base of form-finding strategies. The 3D model is always used to simulate processes, and to define optimized complex shapes. Starting from Gaudí's funicular models, Frei Otto's chain models and reversed Isler's hanging membranes, advances in structurally optimized shape design derive from the widespread availability of digital form-finding tools that make it possible to test several research directions. Through an interdisciplinary collaboration between computer science and architecture, and architects and engineers, the goal of this paper is to test and evaluate different approaches based on computational tools useful for efficient form finding in the design of 3D structural systems by means of an iterative process (Henrique et al. 2020: 171) (Fig. 1).

Digital form finding: iterative process
Full size image
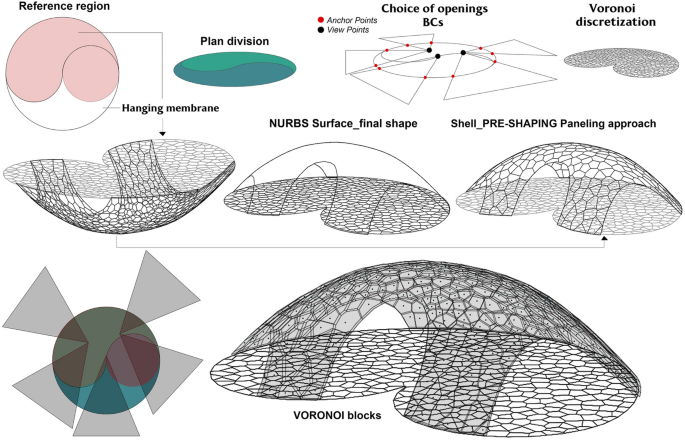
This research work is aimed at designing an inverse hanging shape subdivided in polygonal voussoirs (using Voronoi pattern) by relaxing a planar discrete and elastic system, loaded in each point and anchored along its boundary. The workflow involves three main steps: shaping, discretization (from paneling to digital stereotomy), and structural analysis. Modeling and discretization are managed according to a Visual Programming Language (VPL) algorithmic generative approach (Grasshopper, Rhino) using a specific add-on to simulate forces and anchoring conditions and to model voussoirs (Rippmann et al. 2011b: 183) starting from Voronoi cells (mesh). These models are dynamic systems (Sulpizio et al. 2020: 30) that can be modified in real-time by changing special parameters: geometric pattern, boundary conditions, physical forces, anchor system, loads, materials, stress state.
In this preliminary step, the structural behavior is simulated according to a special digital tool, the live physics engine Kangaroo (see below), which is generally based on mass-spring models. In the third step, a detailed structural analysis is carried out using two types of modeling approaches to check the stress state and to evaluate the equilibrium stability of the shell configuration obtained from the shaping and discretization steps (Fig. 2). The first modeling approach is the finite element method (FEM) implemented in the software suite Abaqus FEA, while the second approach is rigid block (RB) modeling. This second approach was used to evaluate the structural safety against potential local failure mechanisms according to an in-house software tool (named LiABlock_3D), which was developed in MATLAB® (Cascini et al. 2020: 75–94). The code was generated within a research project which is aimed at developing efficient and reliable computational tools based on mathematical programming for the assessment of block structures by nonlinear time-history, static pushover, and limit equilibrium analysis (Portioli 2020: 211–239).

Iterative workflow of structural analysis
Full size image
Traditional architectural shapes are based on geometric rules such as revolution or translation of surfaces, lofting, surfaces intersection, curves interpolation, Boolean transformation, and so on. The 3D modeling technique used to represent the traditional shapes does not allow to define an optimize solution, unlike the form-finding approach.
Instead, the growing complexity of today's architectural design process requires approaches aimed at optimizing processes, minimizing available resources. Curved and complex shapes make it possible to test and to optimize compositional and technological solutions aimed at creating more sustainable architectures. Nowadays, structural analysis using user-friendly digital tools is more accessible in the design phase, although information and data critical interpretation depends on engineering theoretical prerequisites. Special digital tools based on a VPL approach allow designers to independently experiment with funicular systems also in absence of professional expert knowledge (Rippmann 2016: 9). Therefore, the main goal of this approach is to manage the creative process, guaranteeing its feasibility and sustainability. In particular, the main challenge consists in combining shaping with more suitable paneling systems to ensure optimal environmental, structural, economic, and aesthetic performance. According to the digital form-finding approach, parametric generative tools allow designers to explore different shapes by merging the creative phase and structural analysis: the structure defines its own shape according to the equilibrium condition, then the configuration, of a given system under the action of loads.
From Gaudí's catenaries to Heinz Isler's hanging membranes, shapes were realized and tested using material prototypes. The increasing development of special parametric-computational tools allows researchers and designers to simulate the same form-finding approach in the digital environment, optimizing the whole process (Fig. 3). Testing, modifying and validating these configurations in real-time without the onerous manufacturing and verification of material models favors the use of these tools. In addition, digital form finding processes allow global surface deformation to generate optimized shapes characterized by gradual curvature variations, favoring continuity and regularity of shapes (Capone et al. 2014). This approach facilitates the genesis of mechanically optimized complex geometries without resorting to other modeling or post-shaping editing techniques that can undermine system feasibility due to sudden changes in curvature and irregularities (Liu et al. 2006).
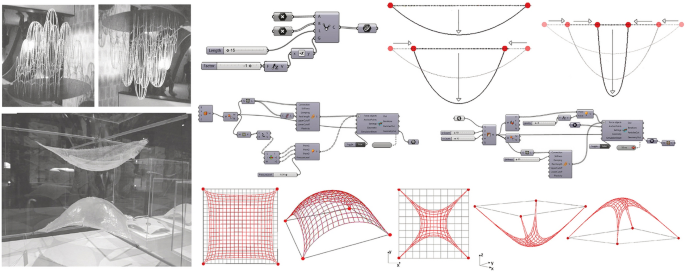
VPL algorithmic generative tools for digital form finding. Special tools (on the right) allow to simulate Gaudí's catenaries and Isler's membranes form finding approach (on the left)
Full size image
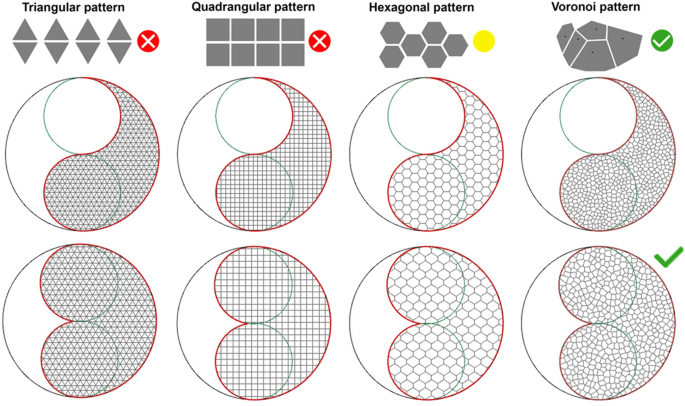
Therefore, the designed hanging membranes were transformed into a corresponding cable net by testing different patterns, regular (triangular, quadrangular and hexagonal), and irregular (Voronoi). Pattern, block shape and distributive layout decisively contribute to the performance of the entire system. This process also allows a possible stereotomic approach for manufacturing complex shapes.
Form Finding: From 2D Boundary to 3D Model
Here we illustrate a digital form-finding process aimed at finding an optimized complex shape designed to cover irregular regions. History provides many examples of using hanging and reverse shapes to design architectural elements employing physical models to obtain structures resistant to compression. Michelangelo (1475–1564), as architect and engineer, reduced the weight of the structure using the method of double skin shell, suggested by Filippo Brunelleschi (1377–1446). Later, in 1580, Giambattista Della Porta (1535–1615) added the height-to-span ratio of the domes by extending their lower parts. Military and civil engineer Simon Stevin (1548–1620) was one of the first to develop the mathematical representation of forces as vectors in his book De Beghinselen der Weeghconst, published in 1586. He illustrated the parallelogram of forces and showed several examples of suspended weights creating funicular shapes in both two and three dimensions. Christopher Wren (1632–1723) and Robert Hooke (1635–1703) worked on the design of a 33 m diameter dome of Saint Paul's Cathedral in London using the suspended chain method and Giovanni Poleni (1683–1761) employed Hooke's method in the evaluation of the 50 m diameter dome of St. Peter's in Rome (Adriaenssens et al. 2014: 35). Friedrich Gosling (1837–1899) used two- and three-dimensional arches in his models in the 1890s. The method was further developed by Antoni Gaudí (1852–1926), who employed small weights suspended from strings to realize models of masonry shells. Frei Otto (1925–2015) used material models to determine the tension in cable networks when a digital approach was unfeasible. Finally, Heinz Isler (1926–2009) designed and built several complex and stable shells inspired by Hooke's method (Timoshenko and Woinowsky-Krieger 1959) starting from simple geometries of reference, according to design or environmental factors.
Contemporary complex architectural shapes cannot be realized according to exact calculations without the use of special tools and of specific knowledges and skills. Mimicking natural shapes allows designers to find optimized complex shapes without intensive calculations (Castro et al. 2020). Therefore, due to the complexity of shell geometries, the historical trials were usually restricted to exactly calculating simple geometries, such as the shapes proposed by Timoshenko and Woinowsky-Krieger (1989). Isler's exceptional ability to model shells according to simple configurations inspired many designers interesting in the field of form finding (Baghdadi et al. 2019: 492–494). This approach provides shaping by hanging and finding simple forms of reference according to the effect of gravity to achieve optimized systems under pure tension (compression), independent of their size, and attaining optimal and economic results. This means that making and testing small physical models can be a quick and practical method. Even major contemporary researchers, such as BRG (Block Research Group, block.arch.ethz.ch/) and Alberto Pugnale (albertopugnale.com/) adopt this logic in designing structurally optimized forms and testing these approaches.
According to all these premises, the boundary of the planar shape that we have chosen for our first tests is a polycentric curve, deriving from the discretization of a circle (Fig. 4).

Searching for a boundary of reference: circle subdivisions
Full size image
In this context, we are going to underline that the planar shape of reference is a result of a design process in which the designer has to define the plan in relation to specific needs. In our case, the final plan derives from the geometric decomposition of a circle and the distribution of strategic openings to guarantee visual permeability, internal/external interaction, and distribution of any internal functional spaces. However, irregular profiles generate curvature variations in 3D membranes by relaxing meshes starting from specific boundary anchoring conditions. The structural behavior of a shell also varies according to the pattern chosen to discretize the planar region of reference (mesh) and the location of the anchor points. By fixing the force weight value and varying the stiffness parameter of springs (Springs component, Kangaroo), the number of isoparametric curves u and v related to the cells number (Panels components > triangle panels, quad panels and hexagon cells, LunchBox) or the number and distribution of Voronoi cells (Mesh components > Voronoi 3D > Points), it is possible to observe morphological variations during the simulation. Stiffness value and relaxation/deformation are inversely proportional: the designer guides the process to control output based on variations in these parameters. By increasing the number of isoparametric curves and setting the stiffness parameter, it is possible to obtain greater deformation deriving from the original flat mesh refinement. In this case, to contain deformation it is possible to increase stiffness value. Therefore, the aim of our research is to test different boundaries and patterns and to compare their structural performances to define the best shaping and paneling strategies to use for the design shape (Fig. 5).
Searching for the boundary of reference according to optimized digital form finding
Full size image
Digital Form Finding and Paneling
Our research illustrates a set of digital form-finding tests to search for favorable geometric conditions aimed at combining formal identity with complex self-supporting surfaces. Computing and verifying design solutions according to a pre-rationalization approach (Shiftner et al. 2012: 216–220) favors dynamic and performing architectural systems. This approach simulates physical forces applied to points and curves that discretize the region of reference: deformation generates different configurations. The digital form-finding simulation makes it possible to interactively manipulate shapes and to visualize Gaussian curvature variations of each configuration in real time, especially for convex configurations that mostly work under compressive stresses. The form-finding approach developed by Isler to manufacture thin hanging and then inverted membranes consists of immersing a fabric anchored at its vertices in a mixture of water and plaster. The relaxed system solidifies by contact with air and the resulting shape can be turned upside down. The form of relaxed membranes depends on the initial planar grid, the boundary and the position of anchor points. The open-source digital tools used for simulating and testing this approach are Rhino and its Grasshopper plug-in, combined with its add-ons Kangaroo, Footnote 1 LunchBox, Footnote 2 Weaverbird Footnote 3 and NGon. Footnote 4 Kangaroo is a live psychics engine to digitally simulate physical forces (force vectors), including the components Unary Forces (strength weight), Catenary (catenaries) and pressure (pneumatic system, compressible gas) acting on points of a discrete input system. The engine also allows the designer to planarize cells (Planarize component) to optimize paneling manufacturing. LunchBox and Weaverbird are special add-ons that make it possible to tessellate surfaces and manipulate meshes. Force weight simulation is enabled by Kangaroo's Unary Force component, which allows us to transform a flat and continuous NURBS surface first into a mesh, and then into a discrete relaxed system physically and structurally like a real fabric lattice. The shaping and paneling steps can be addressed simultaneously or separately. Hence, we have identified two different approaches: post-shaping and pre-shaping paneling. In the post-shaping paneling process, we use a generic grid to divide the irregular planar region, we relax it, and we generate the design surface (mesh). We finally paneling the design surface according to the chosen pattern. Tessellation and block generation independent of the original grid is possible by linking a continuous geometric representation to the thrust network (Lachauer et al. 2010: 3). In contrast, in the pre-shaping paneling approach we use the same pattern to obtain the planar region discretization and the paneling design surface. In this way the mesh of reference and the paneling system will be the same. The experimentation shown in this contribution is based on pre-shaping paneling (Fig. 6).
Post-shaping paneling approach. Tessellation after digital form finding (Lanzara 2019: 221–227)
Full size image
Hanging Membranes and Voronoi Pattern for Optimized Shell
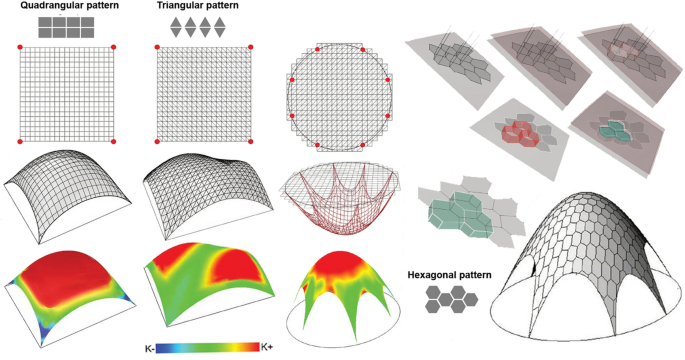
Let's consider the region of reference to extract the planar mesh according to several (regular and irregular) patterns. By relaxing it, we will achieve the final shape that is quite the same as the hanging membrane. Therefore, the first problem is to discretize a flat region delimited by a curved and complex boundary with a regular or irregular pattern. However, the choice of a grid that is regular (triangles, quadrilaterals, hexagons) or irregular (Voronoi) also depends on structural performance. Structural performances of each pattern are verified by the FEM applied to the discrete shell. As stated, convex shells mainly work at compressive stresses (Sasaki 2005). Therefore, to achieve convex shells, virtual weight forces are applied on internal vertices of polygonal cells, and the mesh is constrained at anchor points selected along mesh boundary according to specific design goals. Furthermore, the position of the anchor points also influences the shape curvature. In the case of a planar region with a curved profile, the available digital tools approximate it in a modular grid, recalling the method of exhaustion, a mathematical procedure for calculating areas of planar geometric figures that consists of the construction of a succession of polygons converging to a given figure. Thinking about the shape of a planar grid of reference offers an interesting stimulus to test many different possible solutions. Studies and experiments show that surfaces with a predominantly positive Gaussian curvature allow the distribution of regular flat-convex hexagonal panels.
Hexagonal panel planarization is mainly aimed at finding optimized economic, aesthetic, and constructive solutions to manufacture complex shapes. However, in the architectural field, this pattern is still little used despite its numerous advantages, such as its offset properties useful for creating multilayer systems to promote energy and structural performance of envelopes and facades, and to develop digital stereotomy applications.
Next, the resulting curved region is meshed according to a given number of isoparametric curves u and v, defining its subdivision in both directions. The mesh structure allows us to geometrically simulate fibers of a real elastic membrane. We are transforming the hanging membrane into a corresponding cable net.
Meshes based on regular (triangular, quadrangular, hexagonal) or irregular (Voronoi) patterns are exploded into vertices and curves and transformed into an elastic system (Springs component, Grasshopper, Rhino). Transforming geometric elements into "ideal springs" allows controlling a series of parameters, including stiffness or plasticity of material assumed for simulation, by setting adequate values to prevent a membrane from being "infinitely" relaxed or too rigid. Force is simulated by applying parallel z-axis vectors on each point of the achieved discrete and elastic system: unary forces are applied to each of the points, using oriented vectors. The planar mesh of reference belongs to the xy plane, therefore the vectors representing weight force will be directed downwards. The gravity force action simulation on mesh vertices requires an anchoring system (anchor points) to avoid detachment of the relaxed membrane from tge support. The first tests foresee membrane anchoring along the entire boundary (attempting shape), testing different patterns (triangular, quadrangular, hexagonal and Voronoi), and comparing the results: according to the same parameters, the quadrilateral mesh, unlike the more rigid triangular mesh, allows a more "homogeneous" relaxation, corresponding to a more uniform and almost totally positive Gaussian curvature distribution (Fig. 7).
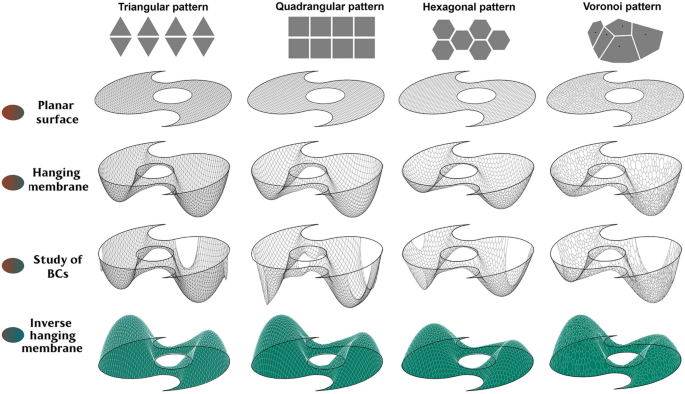
Pre-shaping paneling approach: testing pattern for digital form finding according to design goals
Full size image
Our tests show that the Voronoi pattern is performs better in terms of membrane relaxation and structural performance. A Voronoi tessellation is a subdivision of a plane into cells based on the distance to points in its specific subset. That set of points (called seeds, sites, or generators) is specified beforehand, but for our test, a random set of points was used. Therefore, the Voronoi structure starts from a random distribution of points on the planar region of reference. These points represent vertices of Voronoi cells that populate a closed region. From these points, which are the center of our shape, circles were generated. Their intersections produce the same number of polygons with a different number of edges. Cells along the boundary are open: therefore, it is necessary to transform them into closed polylines, then exploding the meshes to separately select vertices (unary forces application) and edges (springs).
Figure 8 shows the progressive evolution of the final boundary. The covered region is equal to 245 m2, while the whole circular area is equal to 490 m2 and the number of Voronoi cells is equal to 200.
Boundary evolution. Pattern distribution on the planar region of reference
Full size image
Geometry (points, linear connections), forces (unary forces and springs), and anchor points are the input parameters for Kangaroo. The perturbed particles reach equilibrium and flat elastic meshes relax. To distribute arches in the final shell, groups of points distributed along the boundary of the region were excluded. Then, at those points, the membrane is released. The position of arches (height and shape are calibrated through relaxation) were controlled by building a series of optical cones whose vertices are distributed inside the shell to simulate strategic viewpoints to allow system permeability. This approach is aimed at generating a structurally optimized configuration meeting specific functional needs (Fig. 9).
Final solution: structurally optimized configuration and paneling solution meeting specific functional needs
Full size image
From Paneling to Digital Stereotomy
In our research we are testing a design process for the digital manufacturing of an optimized surface using Voronoi blocks. We had to deal with two main questions: the geometric question linked to stereotomy and the structural question. The main topic is how to manufacture a continuous surface that looks like a thin shell structure using blocks.
Offset discrete systems composed of flat polygonal elements allow transformation of cells into volumetric adjacent elements. The faces of these elements can be flat or curved. This advantage allows to evaluate a possible stereotomic approach to manufacture complex shapes.
A stereotomic system, according to the number and shape of elements, can return the curvature of a continuous system of reference without high approximation. Stereotomy is the science of structures of masonry or other materials whose elements are made according to careful prefabrication processes. A stereotomic system subsists in its form by the geometries of its parts, which must be prefabricated to dry-build an organic architectural ensemble. Basically, this science studies projective rules to design shapes aimed at being cut so as to realize complex architectural systems (Fallacara 2007: 36).
It is possible to define three stereotomic principles: prefigurative invariant, to divide a system into parts; technical/geometric invariant, to describe the geometry of a system and its parts; static invariant, to ensure the static balance of the architectural system by dry assembly of its segments (Salvatore 2009: 486). According to these principles, stereotomic design studies the subdivision of a continuous system: the geometry of each element is inextricably dependent on the nature and transformations of the entire system. Thus, the single part strongly depends on the whole configuration. According to these premises, it is interesting to apply these principles to investigate alternative solutions for complex shapes manufacturing.
In offsetting a discrete system resulting from a complex surface, each voussoir will necessarily be different from the others. This technique requires a theoretical treatment starting from principles described in stereotomy treatises both ancient and contemporary (Fallacara 2007; Salvatore 2012). Hence, the relationship between computational design and digital fabrication sets up stereotomy as a very topical science. The main steps (Rippmann et al. 2011a) of the current stereotomy approach are: form finding (shaping), tessellation, segment cutting (voussoirs; see Rippmann and Block 2011b: 183) and assembly. The Block research Group of the ETH Zurich, mentioned earlier, whose research aims to develop methods for the tessellation of complex vaulted systems by the distribution of solid blocks, and the Institute for Computational Design and Construction of the University of Stuttgart emerge among leading research groups engaged in the development of digital stereotomy approaches. Offset-mesh testing demonstrates the utility of the investigation and systematization of the basic theoretical principles of digital stereotomy: stereotomic design inevitably requires knowledge of the geometric rules for controlling the overall morphology of an entire architectural organism and of its parts. Therefore, it is interesting to combine advanced knowledge of complex surfaces and contemporary rationalization techniques with basic knowledge of the science of stereotomy. Figure 10 shows the distribution and a detail of adjacent Voronoi blocks, showing contact faces, edges and vertices. Section 6 presents a discussion of the calculation of the thickness of segments to guarantee the best structural performance.
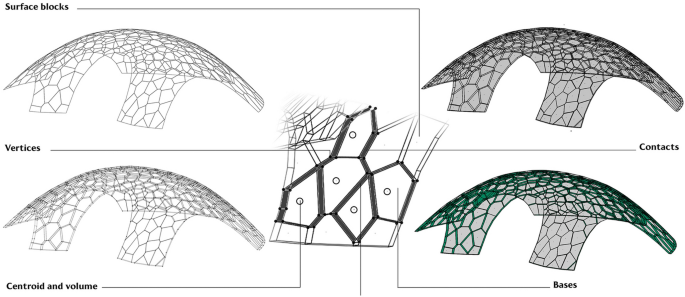
Distribution and detail of adjacent Voronoi blocks, showing contact faces, edges and vertices
Full size image
Structural Analysis
For structural analysis, FEM and RB analyses were carried out to verify the stress distribution and the formation of failure mechanisms when the structure is subjected to load configurations which might be different from those used for the shape optimization study, such as the varying distribution of live loads. In this case, we assumed that the structure is made of stone blocks with a compression strength equal to 20.0 MPa and a tensile strength of 1.0 MPa. For variable loads, the effects of snow loads were considered according to Eurocode 1 (CEN 2003), assuming a total design load of 9 kN/m2 including the effects of self-weight. The FEM model was generated in Abaqus, importing the surface which was obtained from the form-finding study. In this case, a static analysis was carried out adopting an elastic material model (with the Young modulus and Poisson ratio equal to 0.3, respectively). S4R shell elements were used for meshing. The objective of the finite element analysis was to design the thickness of the block vault in order to meet stress verifications. The results of the FEM analysis in terms of minimum and maximum principal stresses (expressed in MPa) are shown in Fig. 11, for a thickness equal to 16 cm.
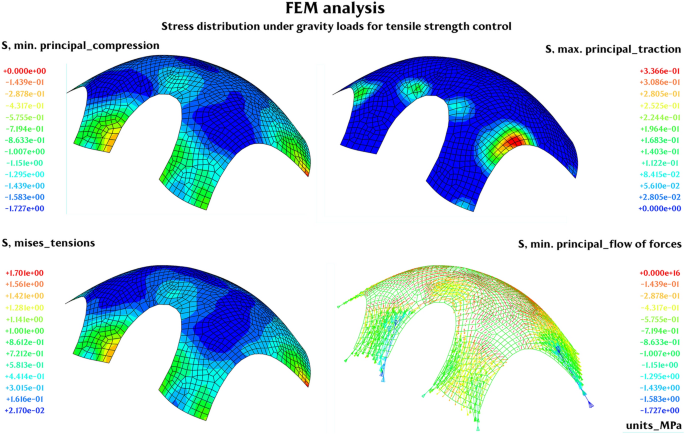
FEM analysis. Stress distribution under gravity loads for tensile strength control
Full size image
In the case of RB analysis, the structural safety was assessed in terms of collapse loads and related failure mechanisms. The structure is idealized into an assemblage of rigid blocks interacting at no-tension, frictional contact interfaces. The limit equilibrium problem corresponding to a failure mechanism is posed as a mathematical programming problem, namely as a second order cone programming problem, following the classic static approaches of limit analysis. The objective function is the collapse load multiplier of variable loads, while the constraints of the optimization problem are the equilibrium conditions at each block and failure conditions at contact interfaces (Cascini et al 2020: 75–94). The results of the rigid block analysis with the LiABlock_3D code are shown in Fig. 12.
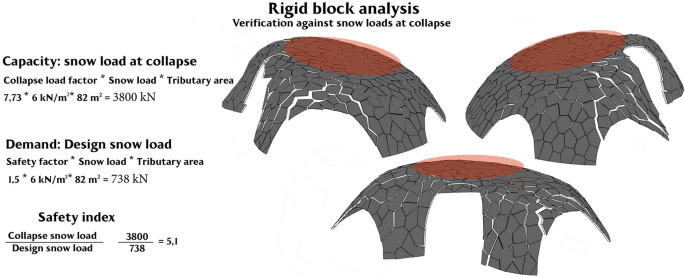
Rigid block analysis. Verification against snow loads at collapse
Full size image
A procedure for extrapolation and export of geometric data was implemented for each structural component. By assigning thicknesses and pattern to the meshes (LunchBox, Weaverbird, NGon) and the center of gravity, the volume of contact surfaces and nodes to each block, it is possible to process and translate resulting data in an electronic spreadsheet. Therefore, we developed a VPL algorithm (Grasshopper, Rhino) to export the necessary data. In this way, we calculated the collapse factor for snow loads, that is, the snow load that induces the activation of a failure mechanism. The safety index, that is, the ratio between snow collapse load and the design load according to Eurocode 1 (CEN 2003), is equal to 3.4. For design purposes and in order to entirely prevent potential sliding phenomena, steel bars were also considered at block interfaces. According to these analyses, 20.0 cm of thickness represents the best solution. Finally, this thickness was assigned to the shell using the Offset Mesh component (NGon add-on) to complete a digital 3D model of the shell (Fig. 13).
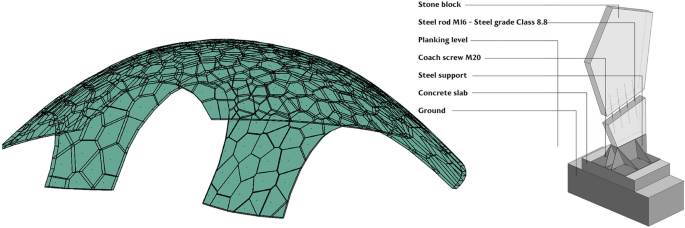
Final optimized discrete shell and ground anchor detail
Full size image
Degital Design Tool Voronoi Diagram
Source: https://link.springer.com/article/10.1007/s00004-021-00566-9
Posted by: martinthessalky.blogspot.com

0 Response to "Degital Design Tool Voronoi Diagram"
Post a Comment